Sommaire ** L’ornementation des coquilles ** L’ornementation des coquilles fossiles ** Modélisation mathématique en 2D,3D et reproduction en 3D ** Le garçon et les coquillages ** Bibliographie
L’ornementation des coquilles
Les coquilles de nombreux gastéropodes marins, principalement ceux vivant dans les régions tropicales, arborent des motifs colorés qui présentent un grand attrait esthétique. Sans évoquer l’extrême diversité des motifs en reliefs tels que les épines, les voiles, les côtes, les bourrelets…
Une telle fulgurance dans la diversité de motifs géométriques sur les coquilles des mollusques et une telle régularité au niveau de chaque espèce, malgré un certain polymorphisme des motifs intra-espèce (voir ci-dessous), a depuis longtemps intrigué et suscité l’intérêt des scientifiques.
Photo de gauche : Lioconcha castrensis (Linnaeus, 1758) Variations intra-espèce « Lioconcha castrensis species group » Sancia E.T. Van des Meij et al – Researchgate juin 2014
Photo de droite : « Variations du motif coloré terrebellum terebellum. Les coquillages de l’Éocène du Bassin parisien » D.Merle et al – Fossiles, Revue française de paléontologie, hors série n° 3.
Alan Turing, mathématicien anglais, (1912-1954) a été le premier à décrire le processus chimique, connu sous le nom de système de réaction-diffusion, qui régit la pigmentation du derme (périostriacum) des coquillages. Ce processus implique le dépôt de molécules chimiques par les cellules du manteau, lors de l’expansion de la coquille d’un mollusque, conduisant ainsi à l’apparition de pigments à la surface du périostriacum.
Alan Turing a fondé sa théorie sur le système de réaction-diffusion ou activation-inhibition. Dans ce cadre, les molécules chimiques régulent la production d’un diffuseur et d’un activateur de motif, ainsi que la production d’un inhibiteur qui entrave la production de l’activateur. Ces deux substances interagissent et influencent mutuellement leur production. La « diffusion » naturelle conduit à un motif homogène, sauf lorsque cette diffusion est contrariée par la « réaction » qui conduit à un motif discontinu. Ce phénomène, connu sous le nom d’ «instabilité de Turing », explique la formation de motifs homogènes ou hétérogènes en fonction des concentrations de ces éléments dans l’espace et dans le temps.
Alan Turing avançait que ce système de réaction-diffusion était également à l’origine de la diversité des motifs observés sur les ailes des papillons, le pelage des mammifères, les pétales de fleurs, ainsi que le motif d’écailles sur une pomme de pin…
Extrait de l'article Wikipedia sur Alan Turing : The Chemical Basis of Morphogenesis (Les Fondements chimiques de la morphogénèse) est un article écrit par Alan Turing en 1952 qui propose un modèle quant au processus naturel d'apparition de non-uniformité au sein d'un milieu de distribution spatiale uniforme et homogène à l'état initial. Sa théorie, que l'on peut voir comme une théorie de la morphogénèse par réaction-diffusion, a servi de modèle de base en biologie théorique et est considérée par certains comme un tout premier pas dans la théorie du chaos. Ce modèle est expliqué au niveau moléculaire pour expliquer la formation de « structures de réaction-diffusion » appelées « structures de Turing » qui consiste principalement en une variation spatiale des concentrations des espèces chimiques (que Turing appelle « morphogènes ») produisant des motifs en bandes ou en taches régulièrement espacées. Il implique deux molécules qui agissent en conjonction dans certaines réactions chimiques : la première agit comme activateur, initiant un processus d'émergence dans l'espace d'un motif particulier et s'auto-amplifiant par rétroaction positive mais stimulant aussi une deuxième molécule agissant comme un inhibiteur et se diffusant plus rapidement, plus loin dans l'espace".
« Indépendamment de la recherche des composants chimiques eux-mêmes, des chercheurs ont proposé, pour la génération des motifs colorés, des modèles physico-chimiques fondés sur des mécanismes de réaction-diffusion. Ces auto-organisations macroscopiques résultent de l’association entre réaction chimique et la simple diffusion moléculaire de ces espèces. Ainsi naissent des ondes propagatrices d’activité chimique, prenant des formes variées (ex. : bandes parallèles, réseaux hexagonaux…). Des simulations assistées par ordinateur montrent que ces modèles reproduisent finement les détails des motifs de coquilles actuelles. Différents types de motifs ont pu ainsi être reproduits avec une grande précision ». Didier Merle and al « Les motifs colorés résiduels des coquilles lutétiennes du bassin de Paris » (2008)
Cette théorie des mécanismes chimiques de type réaction-diffusion, à l’origine de l’ornementation des coquilles a été approfondie par Hans Meinhardt (1938 – 2016), Martin Klinger dans « A model of pattern formation on the shells of molluscs » (1987) et dans un second ouvrage « The Algorithmic Beauty of Sea Shells » (1996).
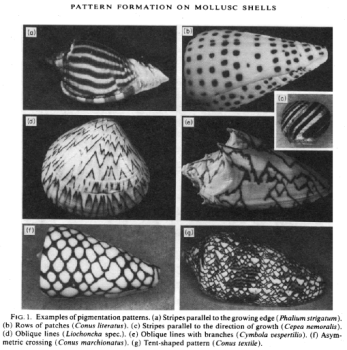
Hans Meinhardt a identifié des modèles génériques de pigmentation des coquilles :
- Bandes parallèles au bord d’accroissement
- Rangées de motifs
- Bandes parallèles à la direction de croissance
- Lignes obliques
- Lignes obliques avec des ramifications
- Croisement asymétrique
- Motif en chapiteau….
Figure 1 : crédit Hans Meinhardt et, Martin Klinger « A model of pattern formation on the shells of molluscs » Ed. Springer (1987)
Un autre intérêt des systèmes de réaction-diffusion réside dans leur aptitude à être traités mathématiquement par des outils d’analyse. En effet les phénomènes de diffusion et de réaction peuvent être modélisés en mathématiques au moyen d’équations. Cette approche ouvre la voie à la reproduction des motifs observés sur les coquilles par le biais de modèles mathématiques.
L’ornementation des coquilles fossiles
"Les motifs résiduels (des coquilles fossiles) sont généralement peu apparents ou invisibles en lumière naturelle, mais peuvent être révélés ou rehaussés grâce à une exposition sous la lumière UV. Un bain préliminaire dans une solution d'hypochlorite de sodium (Eau de Javel) augmente beaucoup les chances d'observation des motifs pendant l'exposition sous la lumière UV. Les investigations· faites par notre équipe au Muséum montrent en premier lieu qu'en utilisant cette technique des motifs colorés résiduels ont été trouvés dans tous les étages du Cénozoïque". MERLE (D.) "Stratotype Lutétien".
Les principaux types motifs d’ornementation des coquilles mis en évidence par Hans Meinhardt et Martin Klinger (voir figure 1 ci-dessus) ont été reconnus chez les fossiles lutétiens examinés par l’équipe de Didier Merle (MNHN) :
- Bandes parallèles au bord d’accroissement (ex. : bandes axiales du gastéropode Tectus mitratus (Deshayes, 1832) et bandes concentriques du bivalve Costacallista laevigata(Lamarck, 1806)).
- Bandes continues, parallèles à la direction de croissance (ex. : bandes spirales du gastéropode Athleta (Volutospina) spinosus (Linné, 1758) et bandes radiales de Costacallista laevigata (Lamarck, 1806)).
- Bandes de tâches parallèles à la direction de croissance (ex. : bandes du gastéropodes Cryptoconus lineolatus (Lamarck, 1804)).
- Lignes obliques ondulantes du gastéropode Mitreola raricosta (Lamarck, 1816).
- Triangles sur fond pigmenté (ex. : triangles de la troisième bande spirale du gastéropodeMitreola maxwelli Le Renard, 1994).
Modélisation mathématique en 2D, 3D
Grace aux travaux de Henry Moseley et de D’Arcy Thompson qui ont décrit mathématiquement la forme des coquilles et les paramètres de la courbe génératrice spécifique à la coquille de chaque espèce de mollusques – voir la spirale chez les mollusques), ainsi que ceux d’Alan Turing et de Hans Meinhardt qui ont élaboré les mécanismes chimiques à l’origine de l’ornementation de coquilles et ont mis en équation des modèles de réaction-diffusion adaptés à chaque type de motifs, et en utilisant les outils de la géométrie différentielle (partie des mathématiques qui étudie les courbes et les surfaces), les chercheurs ont pu modéliser sur ordinateurs en 2, puis en 3 dimensions la géométrie et les motifs de nombreuses coquilles de mollusques.
La forme de l’ouverture et de l’opercule de chaque espèce de mollusque est déterminée par des paramètres mathématiques associés à la forme de la courbe génératrice incluant la forme générale de la coquille, différents angles caractéristiques et la vitesse de croissance… Ces paramètres sont intégrés dans des équations mathématiques complexes dont la résolution permet de modéliser informatiquement la géométrie de la coquille en 2D. Grâce à des outils modernes tels que les imprimantes 3D, il est même possible de créer des répliques tridimensionnelles des coquilles de mollusques, reproduisant à la fois leur forme et leur motif coloré.
Certaines des formes et motifs d’ornementation de coquilles obtenus grâce à ces modélisations mathématiques informatisées sont si fidèles à la réalité que les théories énoncées par Henry Moseley, D’Arcy Thompson, Alan Turing et Hans Meinhardt semblent être valides, bien que les mécanismes chimiques intervenant dans la pigmentation des coquilles n’aient pas encore été directement observés.
Modélisation sur ordinateur en 2D
Modélisation sur ordinateur en 3D
Reproduction en 3D
À l’heure actuelle, de nouveaux outils tels les imprimantes 3D permettent à des chercheurs comme Francesco de Comité de l’Université de Lille) de créer des répliques tridimensionnelles de mollusques, reproduisant à la fois leur forme et leurs motifs colorés :
Et pour finir un joli conte africain "Le garçon et les coquillages" extrait de www.iletaitunehistoire.com
Bibliographie
Henry Moseley » On the Geometrical Forms of Turbinated and Discoid Shells » (1838)
Tracy Thompson « On Growth and Form » (Forme et croissance) (1917).
Alan Turing « The chemical basis of morphogenesis » (1952)
Hans Meinhardt, Martin Klinger « A model of pattern formation on the shells of molluscs » (1987)
Hans Meinhardt « The Algorithmic Beauty of Sea Shells » (1996)
Francesco de Comité « 3D Modelling Seashells » « Modelling Seashells Shapes and Pigmentation Patterns : Experiments with 3D Printing » (2017)
Benjamin Marie « Evolution des biominéralisations nacrées chez les mollusques » (2008)
Pascal Chossat — «Les mathématiques de la morphogénèse (I et II)» — Images des Mathématiques, CNRS, 2012
Paul Valéry « L’homme et la coquille » (1944)
JH Fabre « Souvenirs entomologiques » La Géométrie de l’insecte livre VIII § XVIII (1900)
http://rouxjeanbernard.ch/AM/html/amch65.html
Jean Paul Delahaye « L‘algorithme des coquillages » (Pour la Science mars 2018)
Derek E. Moulton, Alain Goriely et Régis Chirat « Comment les coquillages acquièrent leur forme » (Pour la Science, n°491 29 août 2018) D
Futura-sciences.com « La coquille des mollusques, mémoire de l’environnement »
Didier Merle and al « Les motifs colorés résiduels des coquilles lutétiennes du bassin de Paris » (2008)
Christiane Rousseau « Nautile, nombre d’or et spirale dorée » (2008)
André Stoll « Les spirales » (2020)
Jean-Bernard Roux « Récréations informatique et mathématiques, la coquille des mollusques » http://rouxjeanbernard.ch/AM/html/amch65.html
Robert Ferréol https://mathcurve.com/courbes2d/logarithmic/logarithmic.shtml
Didier Merle and al « Les motifs colorés résiduels des coquilles lutétiennes du bassin de Paris » (2008)
Christiane Rousseau « Nautile, nombre d’or et spirale dorée » (2008)
André Stoll « Les spirales » (2020)
Jean-Bernard Roux « Récréations informatique et mathématiques, la coquille des mollusques » http://rouxjeanbernard.ch/AM/html/amch65.html
Robert Ferréol https://mathcurve.com/courbes2d/logarithmic/logarithmic.shtml
Institut des sciences mathématiques, Université du Québec à Montréal https://accromath.uqam.ca/