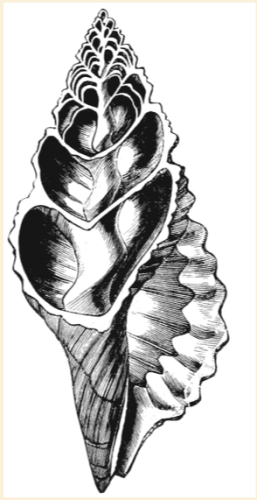
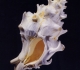
Tchatcheria mirabilis (Angas, 1877)
"Peut-être, ce que nous appelons la perfection dans l’art (et que tous ne recherchent pas, et que plus d’un dédaigne), n’est-elle que le sentiment de désirer ou de trouver, dans une œuvre humaine, cette certitude dans l’exécution, cette nécessité d’origine intérieure, et cette liaison indissoluble et réciproque de la figure avec la matière que le moindre coquillage me fait voir ?" Paul Valéry l’homme et la coquille (1944)
Sommaire
** La fascination pour les coquilles ** La forme des coquilles ** Les spirales ** La fabrication de la coquille ** La composition des coquilles ** Bibliographie
Le terme de coquille est issu du latin classique conchylium via le neutre pluriel du latin vulgaire *conchilia. Ce terme est issu du grec ancien κογχύλιον qui désignait des enveloppes calcaires dures, que ce soit des coquilles d’œufs ou de mollusques.
Les mollusques concernés sont les Conchifères, sous embranchement des mollusques qui possèdent une coquille : les céphalopodes, les gastéropodes, les bivalves, les scaphopodes (notamment les dentales), polyplacophores (notamment les chitons) et les monoplacophores.
La fascination pour les coquilles
La diversité de leurs formes ainsi que l’esthétique de leur ornementation a depuis longtemps provoqué une certaine fascination :
"Passons aux murex et aux coquillages qui ont un test plus solide. La nature s'est fait un jeu de les varier de mille manières. Que de différences dans les nuances ! que de différences dans les formes 1 Ils sont plats, concaves, allongés, échancrés en croissant, arrondis en globe, coupés en demi-globe, élevés en cintre, unis, rugueux, dentelés, striés ; leur sommet se contourne en spirale ; leur rebord s'allonge en pointe, se renverse en dehors, se replie en dedans. Voyez encore : ils sont rayés, chevelus, crêpés, cannelés, divisés en dents de peigne, imbriqués, réticulés, étendus en ligne oblique ou en ligne droite, ramassés, allongés, tortueux, à valves attachées par une charnière peu étendue, réunies sur tout un côté, entr'ouvertes comme si elles allaient se choquer pour applaudir, contournées en forme de cor. Les coquilles dites de Vénus naviguent, et, présentant au vent leur partie concave, elles font voile sur la surface des mers. Les peignes sautent, voltigent hors de l'eau; ils se servent, eux aussi, de leur coquille comme d'une barque. Mais pourquoi m'arrêter à de si petits détails, quand rien n'a plus contribué que la classe des coquillages au luxe et à la dévastation des mœurs? La mer est déjà, de tous les éléments, celui qui coûte le plus cher à la gourmandise, par tant de mets variés, tant de services, tant de poissons savoureux, estimés en raison des périls que courent les pêcheurs. Mais qu'est-ce en comparaison des pourpres, des coquillages et des perles ? C'était peu sans doute de dévorer les dépouilles de la mer; il a fallu encore en charger les mains, les oreilles, la tête, le corps entier des hommes comme des femmes." Pline l'Ancien Histoires Naturelles - Livre 9 § 52
Jean-Henri Fabre célèbre entomologiste a fait part de son admiration et de ses interrogations face à la perfection architecturale de la coquille des mollusques :
"D'autres, avec intelligible, au conflit des pois gonflés substituent le conflit des sphères qui de leurs intersections et par un mécanisme aveugle conduisent au superbe édifice des Abeilles. Un ordre, émanation d'une intelligence attentive à tout, est, à leur sens, hypothèse puérile ; l'énigme des choses s'explique par les seules virtualités du hasard. A ces profonds philosophes, qui nient l'Idée géométrique dominatrice des formes, soumettons le problème de l'Escargot. L'humble mollusque enroule sa coquille suivant les lois d'une courbe connue sous le nom de spirale logarithmique, courbe transcendante en comparaison de laquelle l'hexagone est d'extrême simplicité. Les méditations des géomètres se sont complu à l'étude de cette ligne, si remarquable de propriétés. Comment l'Escargot l'a-t-il prise comme guide de sa rampe à vis ? Y est-il parvenu par des intersections de sphères ou autres combinaisons de formes enchevêtrées l'une dans l'autre ? La sotte idée ne mérite pas qu'on s'y arrête. Avec l'Escargot, pas de conflit entre collaborateurs, pas de pénétrations mutuelles entre édifices similaires et voisins. Tout seul, bien isolé, très pacifiquement et sans songer à rien, il accomplit. sa rampe transcendante avec de la matière glaireuse chargée de calcaire. A-t-il du moins inventé lui-même la savante courbe ? Non, car tous les mollusques à coquille turbinée, ceux de la mer comme ceux des eaux douces et de la terre ferme, suivent les mêmes lois, avec des variations de détail en rapport avec le conoïde sur lequel la spirale type se projette. Les constructeurs de l'époque présente y sont-ils parvenus par le perfectionnement graduel d'un tracé antique, moins correct ? Non, car, dès les premiers âges du globe, la spirale de haute science préside à l'enroulement des coquilles. Les Cératites, les Ammonites et autres mollusques antérieurs à l'apparition de nos continents s'enroulent de la même manière que les Planorbes de nos ruisseaux. La spirale logarithmique du mollusque est vieille comme les siècles. Elle vient de la Géométrie souveraine qui régit le monde, attentive à la cellule de la Guêpe comme à la rampe de l'Escargot. Dans ses ouvrages, la Puissance créatrice toujours géométrise, _'Aéi o théos guéômétréï_ disait Platon." JH Fabre (1823-1915) "Souvenirs entomologiques" La Géométrie de l'insecte livre VIII § XVIII
Ou alors Paul Valéry s’interrogeant sur les mystères de la construction et la perfection de la coquille des mollusques :
"Que constatons-nous ? Le travail intérieur de construction est mystérieusement ordonné. Les cellules sécrétoires du manteau et de sa marge font leur œuvre en mesure : les tours de spire progressent ; le solide s’édifie ; la nacre s’y dépose. Mais le microscope ne montre pas ce qui harmonise les divers points et les divers moments de cet avancement périphérique simultané. La disposition des courbes qui, sillons ou rubans de couleur, suivent la forme, et celle des lignes qui les coupent, font songer à des “géodésiques” et suggèrent l’existence de je ne sais quel “champ de forces”, que nous ne savons pas déceler, et dont l’action imprimerait à la croissance de la coquille l’irrésistible torsion et le progrès rythmique que nous observons dans le produit. Rien, dans notre conscience de nos actions, ne nous permet d’imaginer ce qui module si gracieusement des surfaces, élément par élément, rangée par rangée, sans moyens extérieurs et étrangers à la chose façonnée, et ce qui raccorde à miracle ces courbures, les ajuste, et achève l’œuvre avec une hardiesse, une aisance, une décision, dont les créations les plus souples du potier, ou du fondeur de bronze ne connaissent que de loin leur bonheur. Nos artistes ne tirent point de leur substance la matière de leurs ouvrages, et ils ne tiennent la forme qu’ils poursuivent que d’une application particulière de leur esprit, séparable du tout de leur être. Peut-être, ce que nous appelons la perfection dans l’art (et que tous ne recherchent pas, et que plus d’un dédaigne), n’est-elle que le sentiment de désirer ou de trouver, dans une œuvre humaine, cette certitude dans l’exécution, cette nécessité d’origine intérieure, et cette liaison indissoluble et réciproque de la figure avec la matière que le moindre coquillage me fait voir ?" Paul Valéry « L’homme et la coquille » (1944)
La Forme des coquilles
Section de la spirale de Triton corrugatus, Lam. © Arthur Smith Woodward
Coupe montrant, à l’intérieur d’un mollusque gastéropode, la columelle, axe autour duquel s’articule la structure hélicospirale (spirale hélicoïdale) de l’ensemble de la coquille.
Depuis longtemps, la régularité de la forme des coquillages est remarquée et les termes d’hélice (latin helix, -icis, du grec heliks, -ikos, spirale), de torsion, de spirale pour définir la structure des mollusques sont employés. Déjà Aristote :
"Dans les univalves et dans les bivalves, la partie charnue adhère à la coquille, de telle sorte qu'il faut une certaine force pour l'en détacher. C’est plus facile pour les turbinés. Un caractère commun de la coquille dans tous ces derniers, c'est que c'est l'extrémité de la coquille opposée à la tête qui est toujours tournée en hélice, et que l'enveloppe qui les recouvre est toujours congéniale. Parmi les testacés, les turbinés marchent toujours à droite ; ils ne se meuvent pas dans le sens de leur hélice, mais en sens opposé". Aristote "histoire des animaux" Livre 4 §7
La coquille des gastéropodes s’enroule comme si elle suivait une hélice tracée sur un cône de révolution et dont la projection en deux dimensions sur la base du cône est une spirale logarithmique ; on parle dans ce cas de coquille « turbinée » (en cornet) ou « hélicospirale » (spirale hélicoïdale).
Quant aux céphalopodes, comme les nautiles, les argonautes et la plupart des ammonites, leurs coquilles, ou nacelles pour les argonautes, s’enroulent dans un même plan, ce qui les qualifie de « discoïdes » ou « planispirales ».
Le processus de fabrication des coquilles a depuis longtemps intrigué les scientifiques, mais la démarche scientifique pour étudier la forme des coquilles a réellement commencé avec le Révérend Henry Moseley, un mathématicien anglais (1801/1872) qui a mis en évidence le rôle de la spirale logarithmique dans la formation des coquilles dans son ouvrage « On the Geometrical Forms of Turbinated and Discoid Shells » (1838) : « Il y a une uniformité mécanique observable dans la structure des coquilles d’une même espèce ; elle suggère que la figure génératrice des nouvelles couches augmente en taille en même temps que la chambre en forme de spirale se développe selon une simple loi géométrique. En considérant l’opercule de certaines classes de coquilles, la détermination de cette éventuelle loi semble possible. Continuellement agrandi par l’animal lors de sa croissance, à mesure que la construction de sa coquille avance, l’opercule élargit progressivement la chambre spirale. »
Communication de Elie de Beaumont à la Société Philomatique de Paris 17 avril 1841.
Les observations de Henry Moseley ont été confirmées par des expériences menées par D’Arcy Thompson, un biologiste et mathématicien écossais (1860/1948). Thompson fut le premier à proposer une formulation mathématique décrivant la forme et de la croissance des coquilles hélico-spirales. Cette formulation a été présentée dans son ouvrage intitulé « On Growth and Form » (« Forme et croissance »), publié en 1917 :
« il y a plus de cent ans le chanoine Moseley nous a donné une interprétation mathématique simple de la forme en spirale des coquilles univalves et son article reste un grand classique de l’histoire naturelle. Mais bien d’autres – certains avant lui, certains parfois longtemps après – avaient étudié le problème et avaient entrevu cette même simplicité dans la forme et la structure des coquilles. Aux environs de 1818, Reinecke avait déclaré que la coquille de Nautillus correspondait à une figure géométrique bien précise, dont les différentes chambres se succédaient selon un rapport constant, selon une proportion continue ; Leopold von Buch puis d’autres après lui se rallièrent à cette idée, et poursuivirent même son développement. »
« Bien auparavant, Jan Swammerdam (1637-1680) avait saisi, avec une perspicacité encore plus grande encore, où se trouvait la racine du problème ; en s’appuyant sur quelques exemples variés tels que ceux de Helix ou de Spirula, il montra que la forme des coquilles, comme celle de toutes les autres coquilles en spirale, relevait d’un même type, celui d’une simple tubulure courbée de diverses manières selon des lois mathématiques bien précises ; et, quels que soient les ornements, épines, tubérosités ou autres bandes colorées surajoutées à ces coquilles, il s’agissait toujours en fait du même type de forme, les différences propres à chaque espèce étant d’origine géométrique. »
D’Arcy Thompson réévalue l’influence de l’Évolution (sélection naturelle) en faveur de la physique et de la mécanique dans la formation des organismes vivants. A partir d’exemples comme le flocon de neige, l’alvéole de la ruche, la corne du mammifère, la plume des oiseaux, la nervure de l’aile de libellule, les graines végétales, ainsi que les squelettes de foraminifères ou les coquilles de mollusques, il démontre l’imbrication totale entre les phénomènes biologiques et les phénomènes mécaniques. Il met en évidence que toute cette diversité morphologique est simplement régulée par un petit nombre de lois mathématiques telles que la suite de Fibonacci, le nombre d’or…
« La coquille est en fait la surface engendrée par la révolution, autour d’un axe fixe (la columelle), d’une courbe génératrice fermée dont les dimensions augmentent continûment, mais qui reste en permanence semblable à elle-même sur le plan géométrique ». Jean-Bernard Roux « Récréations informatique et mathématiques, la coquille des mollusques »
« La courbe génératrice … adopte des formes très variées. Elle est circulaire chez Scalaria, Cyclostoma et Spirula ; on peut la considérer comme une portion de cercle chez Natica ou Planorbis. Elle est triangulaire chez Conus ou Thatcheria, et rhomboïde chez Solarium ou Potamides. Très souvent, la courbe génératrice adopte plus ou moins la forme d’une ellipse : chez Oliva et Cypraea, le grand axe de l’ellipse est parallèle à celui de la coquille ; […] et dans de nombreux cas bien documentés, tels que Stomatella, Lamellaria, Sigaretus haliotoides et Haliotis, le grand axe de l’ellipse est oblique par rapport à celui de la coquille. Cette courbe génératrice devient presque une demi-ellipse chez Nautilus pompilius et un peu plus qu’une demi-ellipse chez Nautilus umbilicatus, le grand axe étant dans les deux cas perpendiculaire à l’axe de la coquille » Tracy Thompson « On Growth and Form » (1917).
La forme de l’ouverture et de l’opercule de chaque espèce de mollusque est déterminée par des paramètres mathématiques liés à la forme de la courbe génératrice, tels que la forme générale de la coquille, les différents angles caractérisant la courbe génératrice, et la vitesse de croissance. … Ces différents paramètres sont intégrés dans des équations mathématiques complexes dont la résolution permet de modéliser, grâce à des techniques informatiques, la géométrie de cette coquille en 2 et 3D. Grâce aux nouveaux outils comme les imprimantes 3D, il est possible de créer une réplique tridimensionnelle de cette coquille de mollusque, avec sa forme et son motif coloré. Voir le paragraphe « modélisation mathématique » dans l’ornementation des mollusques.
"Le critère de toute vraie science réside dans l'importance des liens qui l'unissent aux mathématiques". Kant
"Le menuisier du vieux savoir Fait des cercles et des carrés, Tenacement, pour démontrer Comment l'âme doit concevoir Les lois indubitables et féconde Qui sont la règle et la clarté du monde." Emile Verhaeren "Le menuisier" in "Les Villages illusoires", 1895
Les Spirales
« Une sorte de réflexe, nous dit-il, pousse le savant à tenir pour sacrilège la comparaison entre les cicatrisations des tissus vivants et celles des minéraux. Toujours est-il qu’un travail intense rétablit la régularité dans le minéral comme dans l’animal. Je sais comme tout le monde l’abîme qui sépare la matière inerte et la matière vivante, mais j’imagine aussi que l’une et l’autre pourraient présenter des propriétés communes. Je n’ignore pas non plus qu’une nébuleuse qui comprend des millions de mondes et la coquille sécrétée par quelque mollusque marin défient la moindre tentative de comparaison. Pourtant, je les vois toutes deux soumises à la même loi du développement spiral. » Roger Caillois
Les Gastéropodes sont des Mollusques qui, en général, possèdent une coquille conique, spiralée ou hélicoïdale, d’une grande régularité.
On distingue la coquille « hélicospirale » (spirale hélicoïdale) de la coquille « planispirale ».
La plus ancienne des spirales identifiée est la spirale de Théodore de Cyrène (Vᵉ av. J.-C.) qui fut le maître en mathématiques de Platon.
La spirale d’Archimède (287-212 av. J.-C.) part de l’origine et s’étend vers l’infini en une infinité de spires régulièrement espacées ; la distance entre chaque spire est constante.
La spirale logarithmique (étudiée à partir du XVIᵉ siècle par Descartes et Jacques Bernouilli, entre autres) s’enroule infiniment de l’origine vers l’infini en une infinité de spires d’espacement croissant ; la distance entre chaque spire est proportionnelle.
De g. à d. Spirale de Théodore de Cyrène, Spirale d’Archimède, Spirale logarithmique © //mathcurve.com/courbes2d/logarithmic/logarithmic.shtml
Fabrication de la coquille
« Ce fut alors que je me mis à sécréter de la matière calcaire....Je commençai donc à faire la première chose qui me vint à l’esprit, et c’était une coquille. Du bord de ce manteau charnu que j’avais sur le corps, à l’aide de certaines glandes je commençai à faire sortir des sécrétions qui prenaient une courbe bien circulaire, tout autour, jusqu’à ce que je fusse couvert d’un bouclier dur et bariolé, raboteux au dehors et lisse et brillant à l’intérieur. Naturellement je n’avais aucun moyen de contrôler la forme que j’étais en train de faire, je me tenais là toujours accroupi sur moi-même, silencieux et lent, et je sécrétais. Je continuai même après que la coquille m’eut recouvert tout le corps, et ainsi je commençai un autre tour ; en somme ce qui me venait c’était une coquille de celles qui sont tout entortillées en spirale, de celles dont vous croyez quand vous les voyez qu’elles sont très difficiles à faire et, au contraire, il suffit d’insister et de sortir une matière toujours pareille sans interruption, et elles grandissent ainsi un tour après l’autre. » Italo Calvino, Cosmicomics – La spirale - 1965
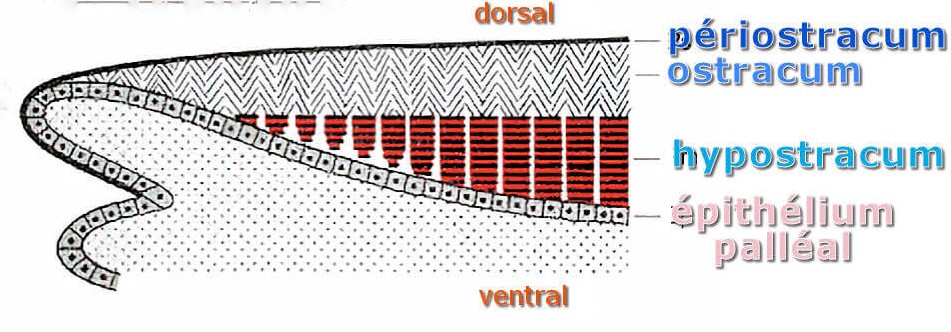
C’est au manteau (pallium, épithélium palléal) du mollusque qu’il incombe de construire la coquille.
Globalement la croissance d’une coquille obéit à 3 principes :
- L’expansion : Lorsque que le mollusque grandit, le manteau sécrète des couches de matériau, généralement du carbonate de calcium au niveau de l’ouverture du coquillage. A mesure qu’il ajoute davantage de matériau, il crée une ouverture de plus en plus large à chaque itération. Ce processus engendre un cône à partir d’un cercle initial
- La rotation : une croissance plus rapide du manteau par rapport à celle du bord de la coquille provoque le dépôt d’un peu plus de matériau d’un côté de l’ouverture et crée de ce fait une rotation de cette ouverture.
- La torsion : L’espace où se dépose le matériau tourne le long du contour du précédent.
>> Les céphalopodes (comme le nautile et de nombreuses ammonites) respectent les deux premiers principes, ce qui les classe parmi les mollusques « planispiralés » .
Pendant leur croissance, le nautile et l’ammonite fabriquent des chambres d’habitation successives qui, bien que plus grandes que les précédentes, sont proportionnelles en taille. Cette croissance reste constante de manière proportionnelle, ce qui correspond au principe de la spirale logarithmique.
>> La majorité des gastéropodes respectent les trois principes, ce qui les classe parmi mollusques « hélicospiralés » .
Pour une illustration sur la columelle qui est la colonne interne d’un mollusque gastéropode, l’axe autour duquel s’articule la structure hélico-spirale (spirale hélicoïdale) de l’ensemble de sa coquille, voir columelle.
Composition de la coquille
La formation des coquilles chez les mollusques implique un processus physiologique complexe appelé biominéralisation, où des organismes vivants produisent des minéraux.
Le principal minéral fabriqué par les mollusques pour former leurs coquilles est le carbonate de calcium (CACO3). Ces structures biominéralisées en carbonate de calcium sont sécrétées couche après couche au niveau de l’ouverture du coquillage par une matrice organique, le manteau (également appelé pallium ou épithélium palléal).

Une coquille est généralement composée de trois couches de compositions différentes :
Périostracum ( n.m. (du grec [peri ] = autour de ; et [ostrakon] = coquille) : Cette couche externe, semblable à l’épiderme, est constituée d’une substance organique appelée conchyoline, sécrétée par le bord du manteau. Le periostracum supporte l’ornementation des coquilles, comme les motifs géométriques colorés. Il est rarement conservé sous forme fossile.
Ostracum : Il s’agit de la partie calcaire de la coquille située sous le périostracum. Cette couche est principalement composée de prismes calcitiques (CaCO3).
Hypostracum : c‘est la couche interne de la coquille des mollusques qui se trouve sous le l’ostracum et du périostracum. Elle est principalement formée de cristaux d’aragonite (CaCO3) disposés perpendiculairement à la surface. Cette couche, associée à la conchyoline, forme la couche de porcelaine et/ou de nacre irisée sur laquelle les muscles s’insèrent.
La combinaison de matière minérale et de matière organique confère aux coquilles des mollusques leur remarquable résistance mécanique.
Il est important de noter que la calcite et l’aragonite sont deux polymorphes du carbonate de calcium (CACO3), la calcite cristallisant dans le système rhomboédrique et l’aragonite cristallisant dans le système orthorhombique.
Le processus physiologique de biominéralisation qui permet aux mollusques d’élaborer cette structure minérale n’est pas encore totalement élucidé.
On pourra lire l’article « Coquille » rédigée par JB Lamarck in « Le Nouveau Dictionnaire d’Histoire Naturelle » Tome VII p 556, 1817. ![]()
Bibliographie
Henry Moseley » On the Geometrical Forms of Turbinated and Discoid Shells » (1838)
Tracy Thompson « On Growth and Form » (Forme et croissance) (1917).
Alan Turing « The chemical basis of morphogenesis » (1952)
Hans Meinhardt, Martin Klinger « A model of pattern formation on the shells of molluscs » (1987)
Hans Meinhardt « The Algorithmic Beauty of Sea Shells » (1996)
Francesco de Comité « 3D Modelling Seashells » « Modelling Seashells Shapes and Pigmentation Patterns : Experiments with 3D Printing » 2017
Benjamin Marie « Evolution des biominéralisations nacrées chez les mollusques » (2008)
Paul Valéry « L’homme et la coquille » (1944)
JH Fabre (1823-1915) « Souvenirs entomologiques » La Géométrie de l’insecte livre VIII § XVIII
http://rouxjeanbernard.ch/AM/html/amch65.html
Jean Paul Delahaye « L‘algorithme des coquillages » (Pour la Science mars 2018)
Derek E. Moulton, Alain Goriely et Régis Chirat « Comment les coquillages acquièrent leur forme » (Pour la Science, n°491 29 août 2018)
Moulton D. E., Goriely A., Chirat R. Mechanics unlocks the morphogenetic puzzle of interlocking bivalved shells. Proceedings of the National Academy of Sciences (2019)
Futura-sciences.com « La coquille des mollusques, mémoire de l’environnement »
Didier Merle and al « Les motifs colorés résiduels des coquilles lutétiennes du bassin de Paris » (2008)
Christiane Rousseau « Nautile, nombre d’or et spirale dorée » (2008)
André Stoll « Les spirales » (2020)
Jean-Bernard Roux « Récréations informatique et mathématiques, la coquille des mollusques » http://rouxjeanbernard.ch/AM/html/amch65.html
Robert Ferréol https://mathcurve.com/courbes2d/logarithmic/logarithmic.shtml
Didier Merle and al « Les motifs colorés résiduels des coquilles lutétiennes du bassin de Paris » (2008)
Christiane Rousseau « Nautile, nombre d’or et spirale dorée » (2008)
André Stoll « Les spirales » (2020)
Jean-Bernard Roux « Récréations informatique et mathématiques, la coquille des mollusques » http://rouxjeanbernard.ch/AM/html/amch65.html
Robert Ferréol https://mathcurve.com/courbes2d/logarithmic/logarithmic.shtml
Institut des sciences mathématiques, Université du Québec à Montréal https://accromath.uqam.ca/